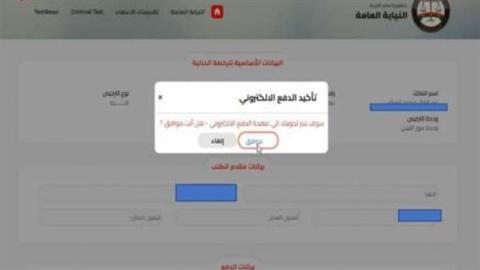
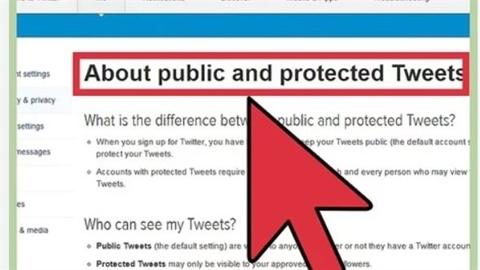
اقرأ أيضا
- قبل مباراة مازيمبي.. شوبير يفجر مفاجأة بشأن
- سعر الدولار بالسوق السوداء اليوم الخميس 25
- بالتزام مع التوقيت الصيفي 2024.. ما هو دعاء
- " كامل الوزير" يشهد توقيع عقد تنفيذ البنية
- مصر تحتفل اليوم بـ ذكرى" تحرير سيناء"
- ردود الفعل حول تغريدة "مشاري العفاسي".. القصة
- أسعار اللحوم فى الأسواق اليوم الخميس 25 أبريل